コンポジット信号、チャンネル足りないと思ったことはありませんか?Lua ブロックへの入力や、マイコン間での情報のやり取り、連結した鉄道車両間での通信や、その他無線通信など、様々な場所でこのような問題に直面することがあるでしょう。この記事ではいかにしてより多くの情報を数値信号・コンポジット信号に詰め込むかという問題への対処法の一つをご紹介します。
結論から書いてしまうと、次の Lua コードを利用して数値信号に30bビットまで詰め込むことができます。なぜこのような処理が必要なのか、このコードが何をしているのか、これから見ていきましょう。
function encode(n) local x = ('f'):unpack(('I3B'):pack(n & 16777215, 66 + 128 * (n >> 29 & 1) + (n >> 24 & 31))) return x end function decode(x) local b, a = ('I3B'):unpack(('f'):pack(x)) local v = 66 <= a and a <= 126 or 194 <= a and a <= 254 return v, v and (a - 66 >> 2 & 32 | a - 66 & 31) << 24 | b or 0 end
Composite Binary ブロック
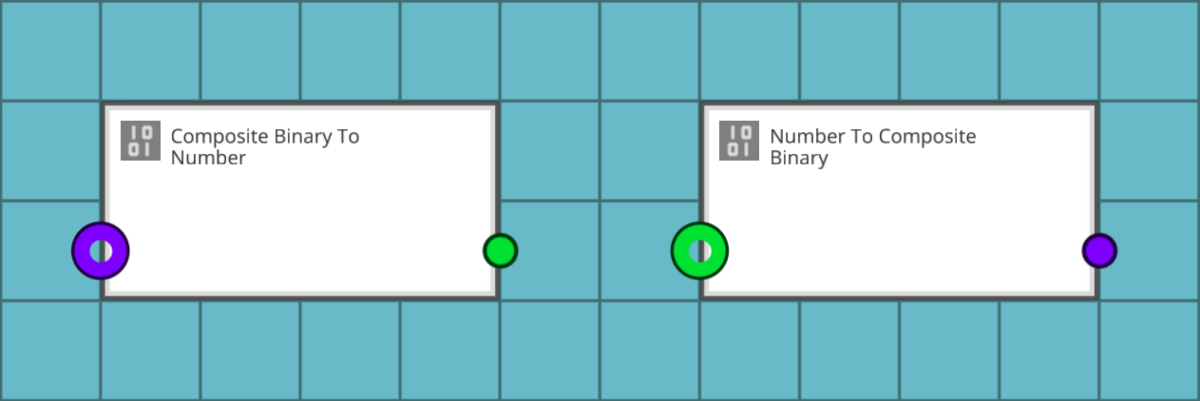
マイコンのロジックにはこのようなブロックが用意されています。”Composite Binary To Number” 、”Number To Composite Binary” とありますが、これはコンポジット信号に含まれるBool信号32個を数値信号に詰め込み、その数値信号を再びBool信号入りのコンポジット信号に戻すブロックです。つまり、これを使うと32ビット分の情報を一旦数値信号1本にまとめることができてしまいます。しかし、このブロックには実は落とし穴があります。
そうだ!これで数値信号にしてからメモリレジスタに保存すればオンオフ信号32個まで1ブロックで保存できるぞ!
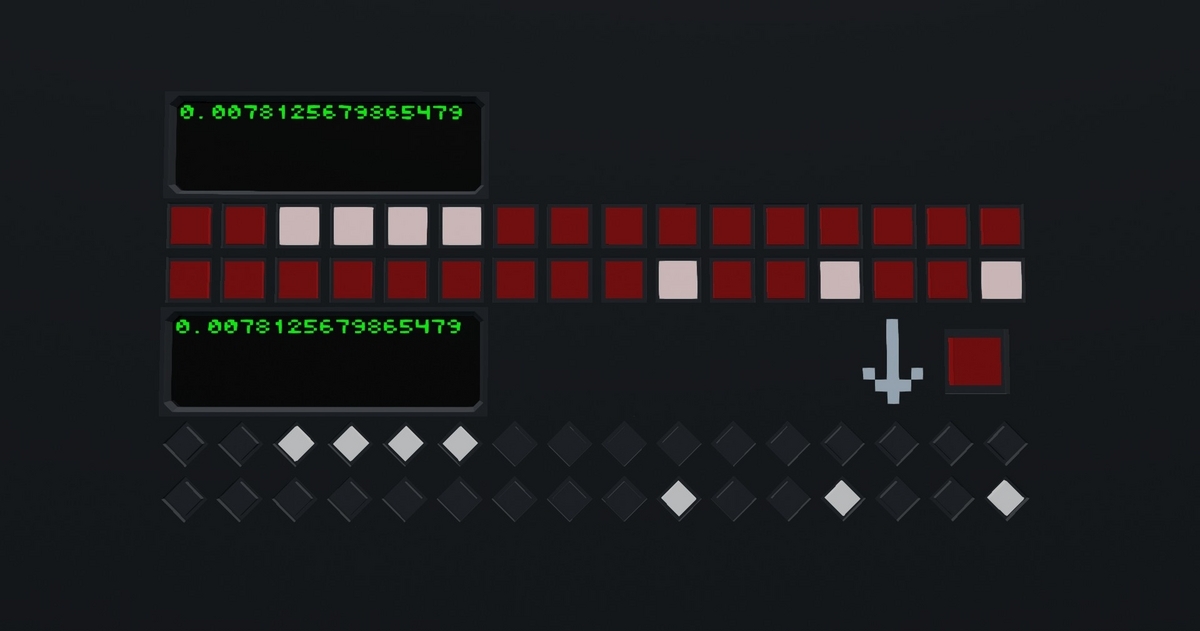
あれれ?一旦ビークルから離れて戻ってきたらなんかおかしいぞ?
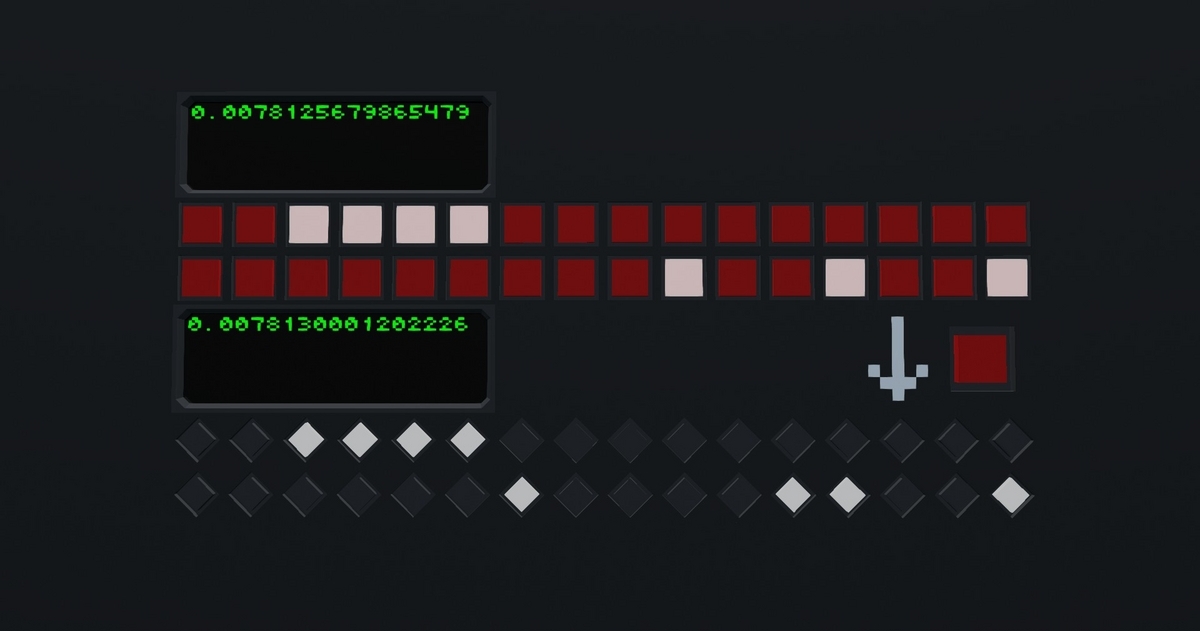
これがこのブロックの落とし穴です。この現象について、詳しく見ていきましょう。
32ビット浮動小数点数
そもそもこのブロックで得られた数値は何なのでしょうか。コンポジットのオンオフ信号をすべてオフにしたら0になりますが、第1チャンネルだけをオンにしたとき1、第2チャンネルだけをオンにしたとき2、第3チャンネルだけをオンにしたとき4…… のようにわかりやすい2進整数値にはなりません。ダイヤル等に表示してみても一見わけのわからない数値が表示されているだけのように思えます。Stormworks の数値信号は32ビットの浮動小数点数、C言語などに馴染みのある方向けに言うとfloat型で表現されていますが、件のブロックでは32個のオンオフの状態をそのまま32ビットの羅列としてそれを数値信号ということにしてしまっている、というような挙動をします。ではこの浮動小数点数とは何なのか、ググればたくさん解説が出てきますが、一応ここでも触れておくことにします。
コンピュータではあらゆる情報を0と1の羅列で表現していることはよく知られていると思います。整数を表現するときは通常の2進数で表せばよいので簡単ですが、実数を表現するときはどうすればよいでしょうか。整数なら上限と下限を定めればその間には有限個しか存在しませんが、実数というのは仮に0以上1以下に限ったとしても無限個ありますので、すべての実数を有限個のビットで表現することは不可能です。では妥協して0.1刻みで表現できればよいとしましょう。この場合、0以上1以下に限るとすれば11通りで済みます。これはいわば「表現したい実数を10倍して、整数に丸めて、2進数で保存」していると言えるでしょう。このようにして実数を表そうとする方法は固定小数点と呼ばれます。用途がはっきりしているなら固定小数点数はシンプルで扱いやすいのですが、刻み幅が固定ということは汎用性が低いということでもあります。例えば、Stormworksでは0以上1以下の数値信号を与えてパーツを制御する場面が多いので、この範囲内でできるだけ細かく表現できるような固定小数点数を数値信号に採用したとします。すると、1より大きい数や負の数は表現できなくなってしまいます。速度センサだとかGPS座標だとかはこういった数値を出力しなければいけないので困ったことになります。
では浮動小数点数とはどのようなものでしょうか。一定の桁数に収まる整数をコンピュータ上で表現するのは可能ですから、それを2つ束ねて実数を表現しようというのが浮動小数点になります。例えば、123.45 という値を表現したいとします。小数点のない値は 12345 で、10進数では5桁の整数で表せます。そして、小数点の位置は左から3桁目と4桁目の間にあり、小数点の位置も整数で表せます。こうすることで、整数を2つ束ねて実数を表現します。もちろん実際には10進数ではなく2進数ですが。
さて、123.45 は $1.2345 \times 10^{2}$ と表すこともできます。こういうのを指数表記などと呼び、 $1.2345$ の部分は仮数部、$2$ の部分は指数部と呼ばれます。仮数部は必ず同じ場所に小数点が来る (そうなるように指数部を決定する) とすると、仮数部の小数点を省略してしまっても構わないということになるので、やっていることはほぼ同じでやはり整数を2つ束ねて実数を表現しています。以上、浮動小数点について2通りの説明をしましたが、うまく解説できた自信はあまりないのでよくわからなければググってよりわかりやすい解説を見てください。
コンピュータで実際によく使われている浮動小数点と言えば、IEEE 754 の規格です。16ビットや64ビットなどいくつかの種類がありますが、Stormworksの数値信号に使われているのは32ビットのものです。C言語(など)に馴染みのある方向けに言えばfloat型です。32ビット浮動小数点数、あるいは単精度浮動小数点数と呼ばれるものでは、最上位の1ビットが符号ビット、つまりプラスマイナスを表しており、その次の8ビットが指数部、残りの23ビットが仮数部となっています。指数部はいわゆるゲタ履き表現であったり、仮数部はいわゆるケチ表現であったりしますが、詳細な説明は省きます。より細かく知りたければ 単精度浮動小数点数 - Wikipedia を参照してください。
なお、指数部が0のときはゼロあるいは非正規化数を表し、指数部が255のときは無限大あるいはNaNを表すということになっています。このうち、後ほど指数部が255の場合について触れます。
この先の話で大事なことは、0に近い値は細かく、0から遠い値は大雑把に表現されるということです。
ちなみに、Composite Binary To Number ブロック、 Number To Composite Binary ブロックと同じ挙動をするLuaを書いてみると次のようになります。
-- Composite Binary To Number function onTick() local n = 0 for i = 0, 31 do n = n | (input.getBool(i + 1) and 1 or 0) << i end local x = ('f'):unpack(('I4'):pack(n & 0xFFFFFFFF)) output.setNumber(1, x) end
-- Number To Composite Binary function onTick() local x = input.getNumber(1) local n = ('I4'):unpack(('f'):pack(x)) for i = 0, 31 do output.setBool(i + 1, n >> i & 1 ~= 0) end end
前者ではまず32個のBool入力を整数に変換します。input.getBool(i + 1) and 1 or 0 では true か false で得られる入力を整数1か0に変換しています。それを後述するビット演算を用いてnの各ビットに配置していき、1個の32ビット整数にしています。('f'):unpack(('I4'):pack(n & 0xFFFFFFFF)) は、整数 n のうち下位32ビットだけを取り出して浮動小数点の実数値に変換するおまじないです。
戻り値を一旦変数 n に格納してからそれを return している部分は冗長に見えるかもしれませんが、unpack の戻り値は複数返ってきますが最初の1つしかいらないので、最初の1つだけを取って残りを捨てるためにこのようにしています。もし unpack の結果をそのまま return すると、unpack の複数の返り値をそのまま返してしまうので、encode の返り値も複数となり思わぬバグの原因になりがちです。
後者では真逆の操作を行ってもとと同じ32個のBool出力に戻します。('I4'):unpack(('f'):pack(x)) は、32ビット浮動小数点数の実数値 x を32ビットの整数値に変換するおまじないです。
ビークルステートファイル
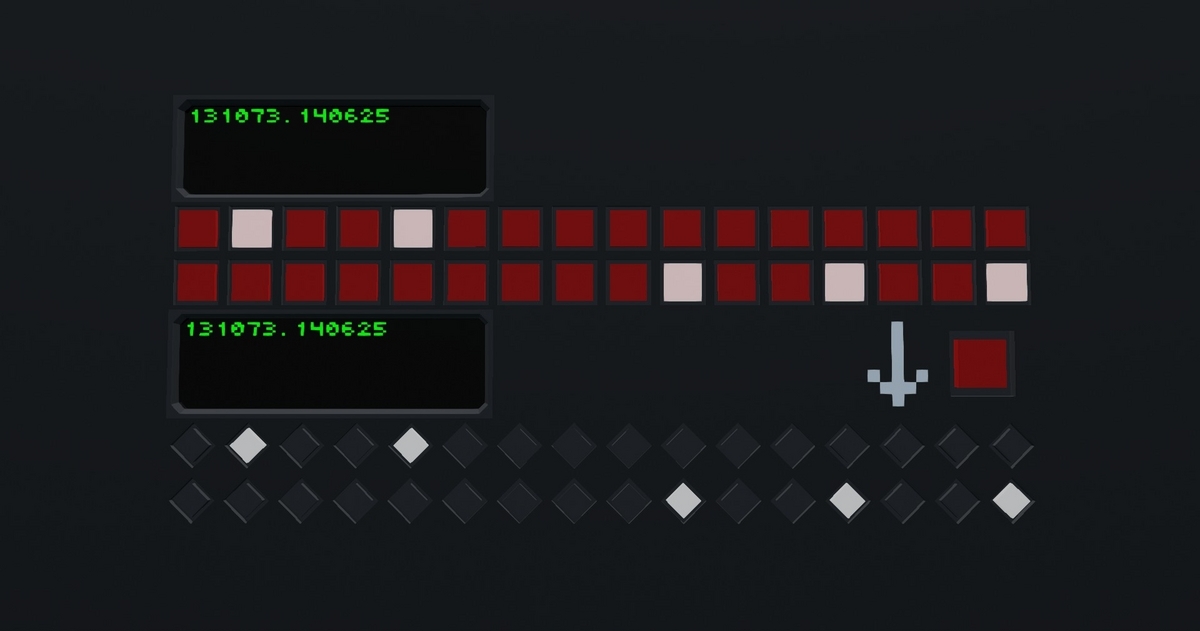
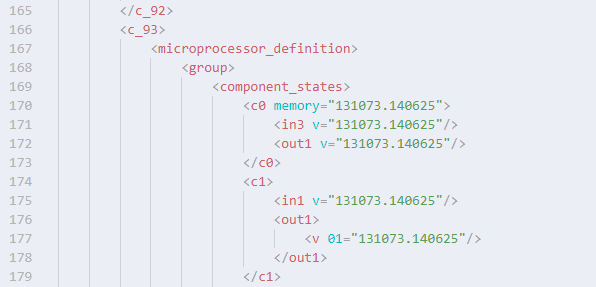
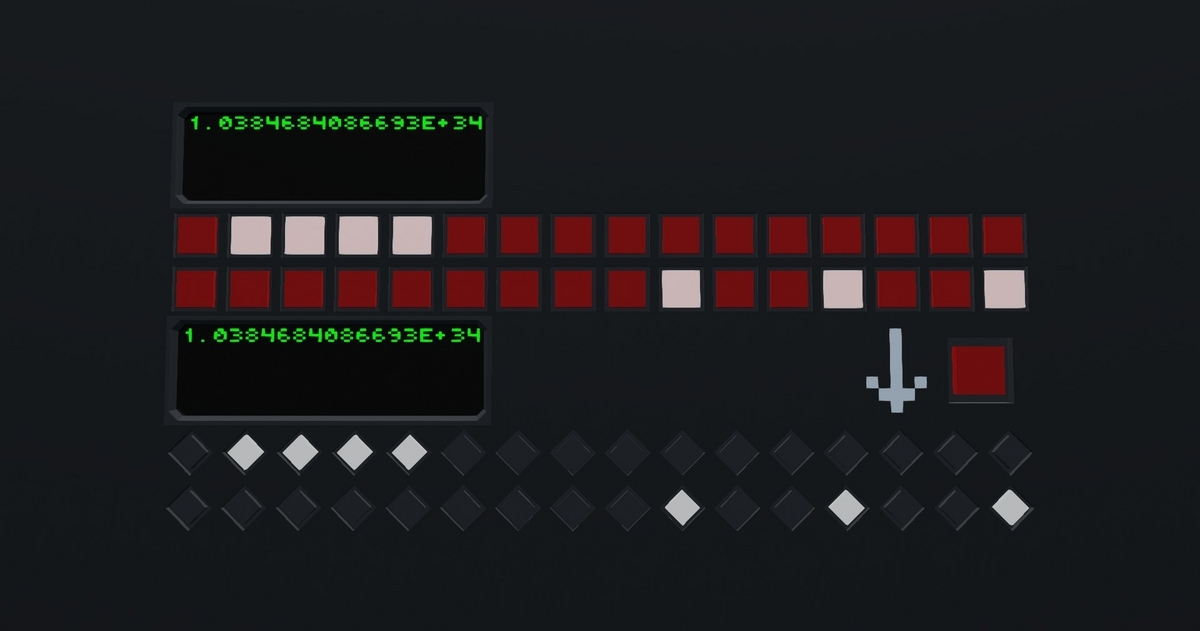
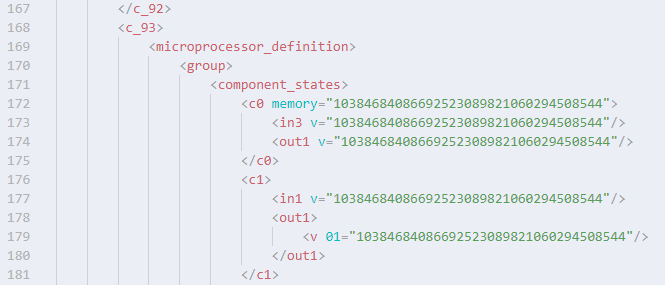
Stormworksの話に戻ってきました。ビークルから離れてロード範囲外になると、そのときのビークルの物理・ロジック状態のスナップショットがXML形式で保存されます。これをビークルステートファイルと呼ぶことにします。メモリレジスタに入っている値もこのビークルステートファイルに保存されますが、本当に正確に保存されているでしょうか。先ほど Composite Binary ブロックを試したときのビークルステートファイルを確認してみましょう。
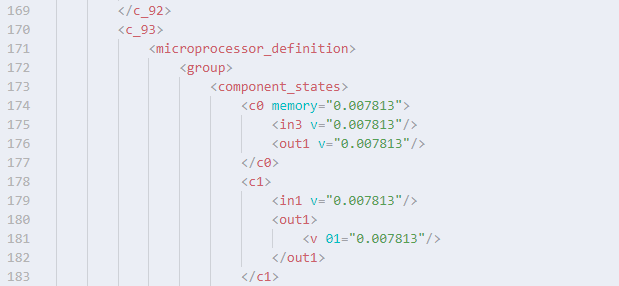
なんと、小数点以下6桁までしか保存されていません。つまりメモリレジスタに値を保存するときは、0に近い値だと精度が落ちて、0から遠い値にしたほうが精度がよくなります。浮動小数点の意味を何もわかっていない実装です。おのれゲオメタ。ひどいはなし。なぜ Composite Binary ブロックを用意しておきながらこの仕様でよしとしたのか理解に苦しみます。
嘆くのはこのくらいにして、この仕様のもとで何ができるか考えましょう。先ほど Composite Binary ブロックを試したときの問題はこれが原因とみられます。ビークルステートファイルに保存するときに値を丸める、つまり一部の情報を捨ててしまっているため、ビークルを再ロードして復元するときに元とまったく同じ値に戻るとは限らないということです。逆に言えば、メモリレジスタに保存さえしないのであれば、ビークルを再ロードした際に一瞬値が乱れるかもしれませんが*1、基本的にComposite Binary ブロックで問題ないかと思われます。とはいえ、一瞬でも乱れると困る場合もあるでしょうし、マルチでどう動作するかもよくわかっていません。ビークルを一旦アンロードしてから再ロードしても値が壊れないようにするためにはどうすればよいでしょうか。
数値信号に何ビット詰め込めるか
ようやく本題です。32ビットの浮動小数点数なんですから32ビット詰め込みたいところですが、後述の理由であえて30ビットに絞ります。仮数部がすべて正しく復元されるためには、仮数部の一番下のビットが0↔1で変化したときにも、丸めた後の値が区別できる必要があります。つまり、仮数部の一番下のビットが表す幅が $0.000001=10^{-6}$ 以上であればよいということになります。指数部の8ビットをそのまま整数として見た値を $E$ とすると、仮数部の一番下のビットが表す幅は $2^{(E-127)-23}$ になります。これらから、欲しい条件は次のように計算できます。
$$ \begin{split} & 2^{(E-127)-23}\geq10^{-6}\\ \Leftrightarrow & E\geq-6\log_2 10+150\fallingdotseq-6\times3.3219+150=130.0684 \end{split} $$
$E$ は整数なので、$E\geq131$ が満たすべき条件ということになります。さらに、$E=255$ のときは、浮動小数点数の仕様として無限大やNaNを表すことになっているため、仮数部の全ビットを正しく復元できる見込みがありません。これを避けるとするなら、$131\leq E\leq254$ が満たすべき条件ということになり、$E$ がとることができる値は124通り、ビット数で表すなら $\left\lfloor\log_2 124\right\rfloor=6$ ビットとなります。符号部1ビットと仮数部23ビットを合わせて24ビット、加えて指数部で6ビットなので、30ビットまではこの条件下で表現できます。以下、この $131\leq E\leq254$ という条件が何度も登場します。
メモリレジスタに保存しても区別できる値の数だけで言えば $2^{30}$ よりも多いのですが、全ビットを互いに独立に立てたり立てなかったりするデータを表現するという条件を課すなら、少なくとも30ビットまでならうまくやる方法が存在することを示すことができました。もしかするともっといいやり方があって31ビットも可能だったりするかもしれませんが、今回は30ビットで十分だということにしておきます。
30ビットで何ができる?
30ビット詰め込めたら何ができるの? という方もいるかもしれません。用途例としてわかりやすいのは、数値信号1本に複数の数値を詰め込むといったような使い方でしょう。例えば、30ビットを10ビットずつ3つに分割したとします。10ビットで表現できる値は $2^{10}=1024$ 通りですから、符号なし整数とすると0以上1023以下の値、10進数で言えば3桁までの値が1つの数値信号に3つまで収まることになります。もし複数の値を送りたくて、値1つあたり1024通りが区別できればよいのなら、コンポジット信号で送るときのチャンネル数を約3分の1に削減することができるということになります。他にも、30ビットを6ビットずつ5個に分割するなら1つあたり64通り、チャンネル数は約5分の1とったようになります。もちろん20ビットと10ビットの2つに分割というようなことも可能です。30ビットをすべて使って1つの値を表すこともできます。浮動小数点形式をそのまま使って整数を表す場合と比較してみると、浮動小数点では $2^{24}=16777216$ までは正確にカウントすることができますが、16777217が表現できず次の値は16777218となってしまうため、10進数での桁数で言えば7桁までなら安全に扱えるがその先は危ういということになります。実際には別に符号部がありますから、浮動小数点数形式で整数を表す場合 $2^{25}-1=33554431$ 通りが限界となります*2。一方で30ビット詰め込む方法をとると、浮動小数点数形式で区別できる整数だけでなく区別できる小数も使うため表現できる値の幅が $2^{30}=1073741824$ 通りまで広がります。10進数で言えば2桁増えて9桁まで安全に扱えるということになります。
ビットをどのように配分するかは用途に合わせて決めることになります。浮動小数点数の規格そのものも、符号部、指数部、仮数部の3種類の整数をそれぞれ1ビット、8ビット、23ビット割り当てて合計32ビットに詰め込んでいると言えるでしょう。なお、送りたい数値が実数値で、なおかつ精度を落とさず送りたいという場合にはチャンネル数を減らすことはできません。精度とチャンネル数削減はトレードオフになるので、精度(桁数)があまり要求されない場面でしかこの方法は使えません。
ではどのようにすれば複数の整数値を1つの整数値に詰め込むことができるでしょうか。2進数の世界で行う場合、Luaのビット演算を使うと比較的簡単に実現できます。例として、入力の1番と2番と3番にそれぞれ8ビット、10ビット、12ビット割り当てて1個の整数にまとめる場合、次のように実装できます。
local a = math.floor(input.getNumber(1)) local b = math.floor(input.getNumber(2)) local c = math.floor(input.getNumber(3)) local n = (a & 255) | (b & 1023) << 8 | (c & 4095) << 18
なお、Luaの数値にはさらに整数と浮動小数点数があります*3。input.getNumber では小数点以下がすべて0であろうとなかろうと浮動小数点数として取り込むので、ビット演算を使えるよう整数に変換するために math.floor を使っています。ビット演算は & と | と << を使っています。
ビットAND演算
& はビットAND演算子で、左右の整数値を2進数で表したとき、各桁ごとに両方1となっている桁だけを1に、それ以外を0にした新たな整数値を返します。6 & 3 を例に見てみると、6=0110(2)、3=0011(2) なので、両方1となっているのは右から2桁目のみとなり、0010(2)=2 という結果になります。
a のうち下位8ビットを取り出したいときは、片方に1が8個並んでおりその上の桁はすべて0となっている数を置けばよいことになります。11111111(2)=255 ですので、a & 255 とすると a のうち8ビットだけを取り出せます。こういうのをビットマスクなどと呼びます。
b & 1023、c & 4095 も同様で、2進数では表すと1023は1が10個、4095は1が12個並んだ数になっています。1が $n$ 個並んだ数は $2^{n}-1$ で求められます。
ビット左シフト演算
<< はビット左シフト演算子で、右側で指定した桁数だけ左側の値の各ビットを左にずらすという意味になります。ずらした結果右、つまり下位のビットが空きますが、この部分は0で埋められます。似た演算子として >> が後に登場しますが、こちらは右シフトです。今回はbのうち10ビットだけを取り出したあと、aのために下位8ビットを空けてその上に移動するので (b & 1023) << 8 としています。
(c & 4095) << 18 も同様で、aとbのために下位18ビットを空けてその上に移動するということです。
ビットOR演算
| はビットOR演算子で、先ほどの & のORバージョンです。左右の整数値を2進数で表したとき、各桁ごとに一方が1となっている桁を1に、両方が0の桁だけを0にした新たな整数値を返します。6 | 3 の例では、6=0110(2)、3=0011(2) なので、0111(2)=7 という結果になります。
今回は予め3つの値が被らないようにマスク、シフトしてありますので、ORで重ね合わせれば3つの値を並べたのと同じことになります。
このようにして得られた30ビット整数値 n は、このまま output.setNumber しても「浮動小数点で表した整数値」として出力されてしまうので24ビットまでしか表せず、情報が失われるおそれがあります。そこで、30ビットを損失なく浮動小数点数に変換する処理を挟むことになります。
浮動小数点数に30ビット詰め込む方法
先ほど30ビットまでは詰め込めるという計算をしたとき、仮数部の23ビットがすべて正しく復元されることを条件としていたので、この23ビットは何も考えずとも安全に使うことができます。これで残りは7ビットです。符号部は浮動小数点数が0以外の値を表すなら正しく復元されるでしょう。もし0を表すなら指数部も0になるはずですが、先ほど求めた条件では $131\leq E\leq254$ なので、指数部 $E$ が0となる場合はそもそも考えなくてよいです。よって符号部もそのまま使うことができます。残り6ビットは指数部で表す必要があります。
問題は指数部の8ビットに残りの6ビットをどう割り当てるかです。$131\leq E\leq254$ という条件を満たさなければなりません。8ビットのうち上位2ビットを1に固定した場合、つまり 11XXXXXX(2) のようにした場合、最小値は 11000000(2)=192 となり、最大値は 11111111(2)=255 となります。255のとき条件を満たさないことになるためこれではよくありません。2ビットをどのように固定しても条件を満たすようなパターンは存在しないと思われます。(証明或いは反例待ってます❤)そこで、ビット演算だけでなく算術演算も使うことにします。6ビットの入力に対して131を足して $E$ を決定するとすれば、$E$ は $131\leq E\leq194$ となり条件を満たします。この方法で送信側をLuaで実装してみると次のようになります。
function encode(n) local x = ('f'):unpack(('I4'):pack((n >> 29 & 1) << 31 | (n >> 23 & 63) + 131 << 23 | n & 8388607)) return x end
30ビットの入力をどのように1ビット、6ビット、23ビットに分割するかは、送信と受信で統一されていれば自由ですが、ここでは上位ビットから1ビット、6ビット、23ビットに分割しています。下位23ビットを取り出すために、n & 8388607 としています。8388607 は2進数で表すと1が23個並んだ数です。次に、下23ビットをすっ飛ばしてその上の6ビットだけを取り出すために、n >> 23 & 63 としています。また、最上位の1ビットを得るため同様に n >> 29 & 1 としています。
仮数部はそのままでよく、符号部も位置を変えて配置しなおせばよいですが、指数部は6ビットだったものを131を足した上で8ビットのスペースに配置することになります。指数部に131を足して、下23ビットを空けてその上に配置するために (n >> 23 & 63) + 131 << 23 としています。算術演算の + は各種ビット演算より優先度が高いので、先に行いたいビット演算にはカッコをつけています。131を足したら最後に23ビット左シフトしています。
ここで、行き先である8ビットのスペースからはみ出すことがないことを確認しなければなりません。6ビットの入力部分 n >> 23 & 63 が最大値63をとったとしても、131を足して194となり、8ビットの限界である255より小さいので問題ありません。
符号部を32ビット目に配置するために、(n >> 29 & 1) << 31 としていますが、これも同様です。最後に、3種類の値をすべて結合するために | 演算子を使います。
このencode関数を使う際には、まず送り出したい情報を30ビット整数に配置し、この関数で浮動小数点数値に変換し、その値を output.setNumber() でLuaの外に出します。あとはそのコンポジット信号なり数値信号なりを通信相手に何らかの手段(マイコン内別Luaやビークル内別マイコンへロジック接続、別ビークルへコネクタまたは無線などなど……)で届けて、受信側のLua関数に入れることになります。
ちなみに、この方法で出力した浮動小数点数の値は0になることはありません。指数部が131以上なので絶対値が16以上の値しか出てこないためです。このことから、受信側ではもし0を受け取った場合信号が届いていないという判定をすることもできます。
受信側では、指数部の8ビットを取り出してから131を引いて6ビットにし、符号部・仮数部と結合して30ビットの整数値に戻します。
function decode(x) local n = ('I4'):unpack(('f'):pack(x)) return (n >> 31 & 1) << 29 | (((n >> 23 & 255) - 131) & 63) << 23 | n & 8388607 end
受信側と逆の操作を行うため、指数部を取り出してから131を引いているのが (n >> 23 & 255) - 131 の部分で、さらに & 63 とすることで6ビットだけを取り出します。仮数部はそのまま、符号部は位置を変えて並べています。先ほどのencode関数が本来出力しないはずの値でも例外処理などは行いませんのでご注意ください。decode関数に0.0を入れても返ってくる値は全ビット0とは限りません。
それでは、先ほどと同じコンポジット1番と2番と3番にそれぞれ8ビット、10ビット、12ビット割り当てる場合について、送信側と受信側のLuaをそれぞれ見てみましょう。
-- 送信側 function encode(n) local x = ('f'):unpack(('I4'):pack((n >> 29 & 1) << 31 | (n >> 23 & 63) + 131 << 23 | n & 8388607)) return x end function onTick() local a = math.floor(input.getNumber(1)) local b = math.floor(input.getNumber(2)) local c = math.floor(input.getNumber(3)) output.setNumber(1, encode((a & 255) | (b & 1023) << 8 | (c & 4095) << 18)) end
-- 受信側 function decode(x) local n = ('I4'):unpack(('f'):pack(x)) return (n >> 31 & 1) << 29 | (((n >> 23 & 255) - 131) & 63) << 23 | n & 8388607 end function onTick() local p = decode(input.getNumber(1)) output.setNumber(1, p & 255) output.setNumber(2, p >> 8 & 1023) output.setNumber(3, p >> 18 & 4095) end
送信側のLuaは先ほどの例にencode関数を付け加えて、output.setNumber で3つの値をまとめた浮動小数点数値を出力コンポジットの1番だけに出力しています。受信側では、コンポジットの1番だけを読み込んでdecode関数に通し、得られた30ビット整数値を分解して output.setNumber でコンポジット1番と2番と3番に出力しています。こうすることで、3つの数値を一旦1つの数値信号にまとめ、その後バラして再び3つの数値に戻すことができています。ただし、小数を入力しても切り捨てられてしまったり、1番に256以上や0未満の値を与えるなどするとオーバーフローして違う値が送られてしまったりします。繰り返しになりますが、実際に使うときには用途に合わせてビットを割り当てる必要があります。
30ビットより少し多く詰め込む方法
これで話は終わりではありません。これまで30ビットが限界と言ってきましたが、実は区別できる値の数は $2^{30}$ 個よりもいくらか多くあります。30ビット詰め込みの場合は $131\leq E\leq194$ の範囲しか使っていませんでした。$131\leq E\leq254$ というのが仮数部のビットがすべて保存される十分条件でしたから、195から254までの範囲はまだ活用できていないことになります。実際、$131\leq E\leq254$ の範囲をフル活用すれば区別できる値は $124\times2^{24}$ 通りあることになります。$\log_2\left(124\times2^{24}\right)\fallingdotseq30.954$ ですから、本当は約30.954ビットくらいということになります。($131\leq E\leq254$ もあくまで十分条件にすぎないため、本当に本当の限界はもう少し先だと思われます。) ギリギリ31ビットに届かないため2進数の桁数では30ビットと言わざるを得ませんが、無駄になっている分を活用する方法も一応あります。
131以上254以下124通りの整数値と、残りの24ビット分で分割し、2つの値を束ねたものとして扱うことで30ビットより少し多い分を使い切ることができます。実用上、先ほど紹介した30ビットの方式でも30ビット全部を1つの値で使いたいということはあまりなく、いくつかの部分に分割して複数の値を束ねたものとして使うことが多いでしょう。分割したうちの1つが124通りの中に収まるなら、それをそこに割り当てて、残りで24ビットを分け合うという使い方ができます。124通り+24ビットという構成でなくとも、少し工夫すれば62通り+25ビットとか、31通り+26ビットとか、15通り+27ビットというように分けることもできます。全体で30ビットとしてしまった場合、例えば26ビット使ったあとに残るのは4ビット=16通りなので、ここに31通りまで入るのなら少しお得です。コード自体は先ほど紹介したものの指数部関連の部分を少しいじるだけです。
少しシンプルに30ビット詰め込む方法
今までは上位から符号部1ビット、指数部8ビット、仮数部23ビットの3つの部分に分割して浮動小数点数値を組み立てていました。しかし、上位8ビットと下位24ビットの2分割にすることでコードを少しシンプルにすることもできます。浮動小数点の上位8ビットというのは、符号部1ビットと指数部上位7ビットに、下位24ビットは指数部下位1ビットと仮数部23ビットにあたります。指数部の最下位ビットだけを切り離して上は符号部と一緒に、下は仮数部と一緒に扱うということです。この場合、上の8ビットはどのような値にする必要があるでしょうか。下の24ビットがどんな値をとっても、指数部が $131\leq E\leq254$ という条件を満たしてほしいのでした。指数部の上位7ビットが表す整数値を $E'$ とすると、$E'=\left\lfloor \frac{E}{2}\right\rfloor$ ですので、$66\leq E'\leq126$ というのが要求する条件です。この上に符号部1ビットがくっつくので、最終的な上位8ビットの値を $A$ とすると $66\leq A\leq126,194\leq A\leq254$ というのが上の8ビットが満たすべき条件です。この条件を満たす $A$ は122通りになります。先ほど、124通り+24ビットという方式を紹介しましたが、こちらの方式でも122通り+24ビットが確保できます。この方式でのLuaコードを次に示します。
function encode(a, b) if a < 66 or 126 < a and a < 194 or 254 < a then -- aが無効なときの例外処理 return 0 end local x = ('f'):unpack(('I3B'):pack(b & 16777215, a & 255)) return x end function decode(x) local b, a = ('I3B'):unpack(('f'):pack(x)) return a, b end
今まで 'I4' と書いていたところが 'I3B' となりました。I4は4バイト=32ビットの符号なし整数を意味していましたが、今回は1バイトと3バイトで分割してもよいので、I3Bとなりました。I3は3バイト符号なし整数、Bは1バイト符号なし整数を意味します。また、下位のほうが先に来ます。
例外処理のif文が増えてしまいましたが、aに変な値が紛れ込まない自信があるならこれは削除してもよいです。使用には少々注意が必要になりますが、その部分を除くとかなりスッキリしたコードになったと思います。
では、この方式をベースに入出力を30ビット整数1個にしてみましょう。122通りの部分に6ビット=64通りの値を入れればよいのですが、その条件が少しややこしいのでした。下位24ビットはそのままですが、上位8ビットについては n >> 24 & 31 で25ビット目から29ビット目までを取り出し、これに66を加えてから、n >> 29 & 1 で最後残った1ビットを取り出し、このビットが1なら128を加えます。結果として 66 + 128 * (n >> 29 & 1) + (n >> 24 & 31) というコードになりました。128を掛けるところは7ビット左シフトでも構いません。
function encode(n) local x = ('f'):unpack(('I3B'):pack(n & 16777215, 66 + 128 * (n >> 29 & 1) + (n >> 24 & 31))) return x end function decode(x) local b, a = ('I3B'):unpack(('f'):pack(x)) local v = 66 <= a and a <= 126 or 194 <= a and a <= 254 return v, v and (a - 66 >> 2 & 32 | a - 66 & 31) << 24 | b or 0 end
このコードは実際に私が使用しているものなので、decodeの第1戻り値では有効な値かどうかをboolで返し、第2戻り値で整数値を返しています。また、入力が有効でない場合は0になるようにしています。実際に使用するときはこのような処理を挟んだほうが致命的なバグを回避しやすく、バグがあるとき発見も容易になります。
まとめ
私が実際に使っているのは最後に紹介した方式です。開発中の電車用システムの車両間通信では、SW-TCS規格の連結器を採用した車両同士で通信するためコンポジット2本しか通信に使えませんが、これを最大限まで活用するために時分割多重化と組み合わせて使用しています。また、高原のな氏らによる「N-TRACS 宗弥急行」(近日公開予定)ではビークルとして設置されるCTC卓とアドオンLuaの間で数十個*4のフラグのやり取りが必要になりましたが、今回紹介した方法を使って数個のキーパッドとダイヤルでアドオンLuaとの送受信を行っています。浮動小数点数どうこうの部分を理解していなくても最低限整数のビット演算についてわかっていれば今回紹介したLuaの関数をコピペで使うことができますので、Stormworksで大きなデータをやり取りするときは時分割多重化とあわせてこの方法も使ってみてください。ここまで書いていて、もしかすると時分割多重化のほうの解説も需要があるかも?なんて思いました。