概要
Stormworks で自動操縦で編隊飛行をする飛行機を作りました。リーダー機から一定の位置関係を維持するように飛行し、リーダー機の上昇・降下・旋回などにも追従します。リーダー機は Physics Sensor のコンポジット信号をそのまま無線で送信するのみで、追従機側で様々な計算を行います。リーダー機の Physics Sensor 信号とは別にもう1つ無線を使用して、リーダー機側からでも追従機側からでも外からでも手持ちリモコンで位置関係を調整することができます。 起動時の条件は、両機とも離陸済み、目視できる程度の距離、進行方向は大まかに一致、速度と高度はずれていてもよし、としています。起動したら追従機は徐々に距離を縮めて、リーダー機に衝突しないようにリーダー機に接近します。目標相対位置は3次元ベクトルで指定して、リーダー機の位置・回転に追従します。

↓動画はこちら
ベース機体
既に編隊飛行マルチで実績のある練習機をベースとします。私はビークルに名前をつけるのを面倒くさがるので名前はありませんが、ファイル名は hikouki20 になっています。この機体は角速度ベースの飛行制御を採用しており、ロールは速度によらず同じような操縦感覚、ピッチは同じような操作で同じようなGになるように速度に応じて角速度を調節します。操縦しながらトリムをとる必要はなく、手を離せば直進するようにできています。操縦しやすくなるように制御しており、編隊飛行マルチでは背面飛行で編隊を維持したり、他の機体に接近して乗り移ったりなども可能です。既に角速度制御を確立している機体を使用することで、編隊飛行マイコンからは操縦翼面そのものではなく角速度を出力すればよく、編隊飛行のための制御に集中できます。

システム構成
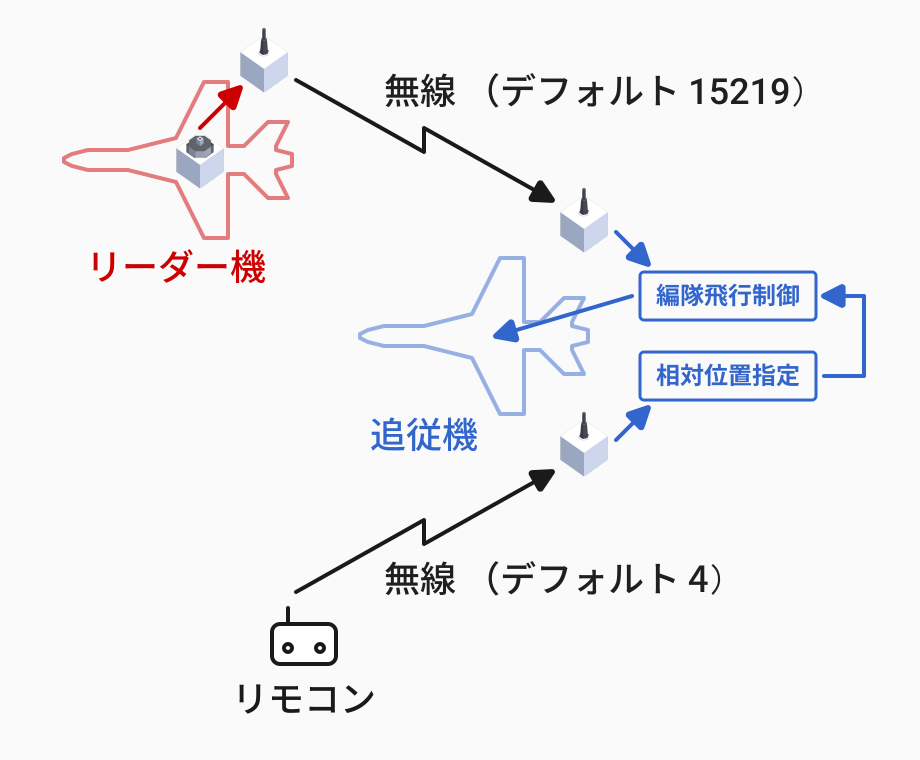
無線は2種類の周波数を使用します。周波数は機体をスポーンしたままのデフォルト状態で 15219 と 4 を使うことにしています。スポーン後に後席右側のキーパッドとボタンで変更できるようにしています。無線 15219 ではリーダー機が Physics Sensor の信号をそのまま送信、無線 4 ではリモコンで相対位置を調整するようにしています。相対位置のデフォルト値はマイコンプロパティ指定で、左後方 (-10, -2, -10) にしています。
実装
本制御は次の要素に分解して考えます。
- リーダー機の Physics Sensor を受信
- 目標相対位置のリモコン調整
- 上2つと自機の Physics Sensor を組み合わせて、目標位置と目標姿勢を計算
- リーダー機の速度に目標位置までの距離で補正をかけた目標速度を計算
- 目標速度からエンジンの制御 (済)
- 目標姿勢と現在姿勢の差分から、ロールピッチヨー各軸の目標角速度を計算
- 角速度をから操縦翼面へのPID制御 (済)
今回肝となるのは、両機の Physics Sensor 信号から各軸の角速度出力とスロットル出力を計算する部分で、この計算は1つの Lua で行っています。まずは記号を定義しておきます。リーダー機のローカル座標系、自機のローカル座標系、グローバル座標系が混在するので注意してください。ローカルベクトルに左から回転行列を書けるとグローバルになります。
- $\mathbb{p}_l$: リーダー機の位置 (グローバル)
- $R_l$: リーダー機の回転行列
- $\mathbb{v}_l$: リーダー機の速度 (リーダー機ローカル)
- $\mathbb{\omega}_l$: リーダー機の角速度
- $\mathbb{p}_s$: 自機の位置 (グローバル)
- $R_s$: 自機の回転行列
- $\mathbb{v}_s$: 自機の速度 (自機ローカル)
- $\mathbb{\omega}_s$: 自機の角速度
- $\mathbb{r}$: 目標相対位置 (リーダー機ローカル)
ピッチ・ヨー制御
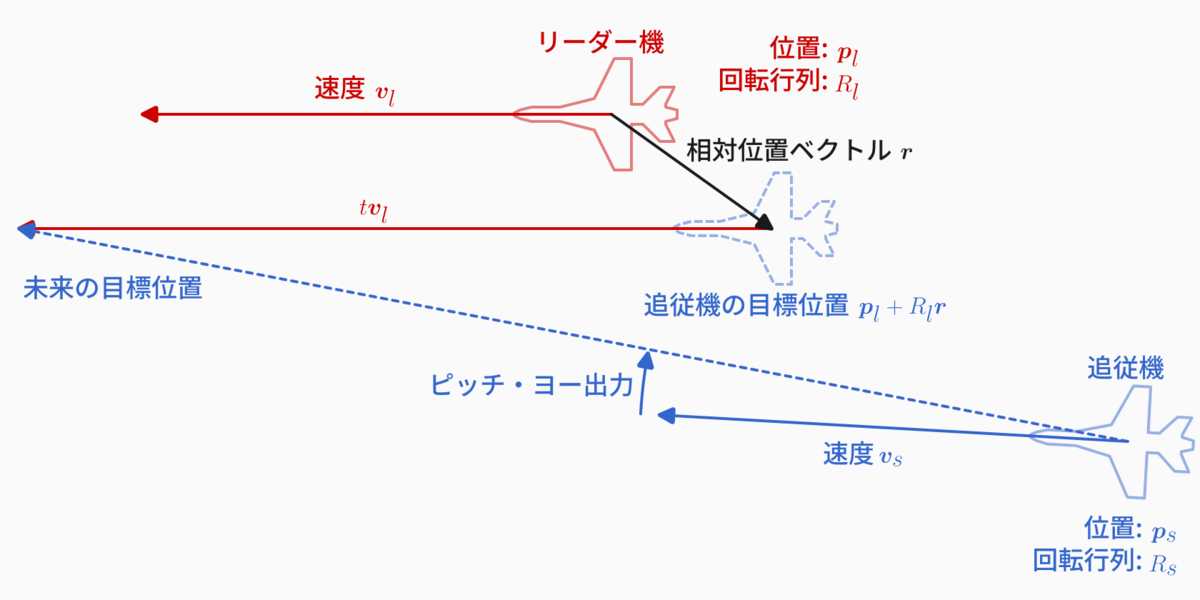
$\mathbb{p}_t=\mathbb{p}_l+R_l\mathbb{r}$ で目標位置を計算することができ、$R_s^\top\left(\mathbb{p}_t-\mathbb{p}_s\right)$ とすれば機首を向けるべき方向がわかるような気がしますが、これでは目標位置に到達したときに零ベクトルとなり向きが不安定になります。そこで、機首は未来の目標位置に向ける制御を行います。$t$ 秒後の未来の目標位置を $\mathbb{p}_tf=\mathbb{p}_t+t\mathbb{v}_l$ として (実際にはリーダー機の旋回も考慮し大雑把に近似したものにしています) 、$R_s^\top\left(\mathbb{p}_tf-\mathbb{p}_s\right)\times\mathbb{v}_s$ として得られるベクトルが、機首を $\mathbb{p}_tf$ に向けるための回転軸ということになります。そのX成分をピッチ、Y成分をヨー出力に繋げば目標位置に機首を向ける制御が達成できます。
ロール制御
機首を目標位置に向ける制御をピッチとヨーで行ったので、ロール制御は別の方法で決定しなければなりません。そこで、編隊飛行したときの美しさも考慮し、リーダー機のロールに合わせることとします。自機とリーダー機の回転の差分を取得し、そのロール成分を取り出して出力に繋ぐことにします。回転行列 $R_lR_s^\top$ の回転軸ベクトルを取得し、自機のローカル系に直すため $R_s^\top$ を左から掛けてZ成分を取り出すことで、ロール出力を得ます。
速度制御
機首は未来の予測目標位置に向けましたが、速度は(未来のではなく)現在の目標位置 $\mathbb{p}_t$ に合わせます。既に編隊飛行が成立した状態なら速度はリーダー機と一致しているはずなので、リーダー機の速度に合わせるのを基本として、目標位置より後ろならやや速く、前に出ていたらやや遅く調整します。また、旋回中は旋回内側は遅く、外側は速くなるはずなので、リーダー機の角速度と相対位置ベクトルも考慮して補正します。その補正を組み込むと、編隊成立状態での目標速度は $R_s^\top\left(R_l\mathbb{v}_l+\omega_l\times\left(R_l\mathbb{r}\right)\right)$ のZ成分になり、これに目標位置までのローカルベクトルのZ成分で前後のずれ分の補正に $R_l^\top\left(\mathbb{p}_s-\mathbb{p}_t\right)$ のZ成分を適当に乗せて実際の目標速度とします。
接近時の衝突抑制制御
距離が遠い状態で編隊飛行をオンにしていきなり目標位置に向かって飛行すると、オーバーシュートしてリーダー機に衝突することが容易に想像できます。しかし、きちんと衝突回避しようとするとなかなか面倒*1ですので、編隊が成立するまでは目標位置の計算に使う相対位置ベクトルに係数を掛けて大きくしておきます。この係数は適当に実験で $1+0.25\frac{\max\left(|\mathbb{p}_t-\mathbb{p}_s|-2,0\right)}{|\mathbb{r}|}$ にすることにしました。0.25 の部分で接近スピードが決まり、0 に近いほど早く、1に近いほど遅くなるはずです。
Lua
ロール、ピッチ、ヨー、速度の制御方針が定まったので、Lua を書いていきます。入出力は次の通りです。
入力
- B1: 起動
- N1-N12: リーダー機から受信した Physics Sensor 信号 (位置、オイラー角、速度、角速度)
- N13-N21: 自機の Physics Sensor 信号 (位置、オイラー角、速度)
- N22-24: 目標相対位置
出力
- B1: 起動
- N1: ロール目標角速度
- N2: ピッチ目標角速度
- N3: ヨー目標角速度
- N4: 目標速度偏差
gB,gN,sB,sN=input.getBool,input.getNumber,output.setBool,output.setNumber function clamp(x,a,b) return math.min(math.max(x,a),b) end function onTick() enable=gB(1) -- 編隊飛行制御の起動信号 pos_l={gN(1),gN(2),gN(3)} -- リーダー機の位置 (グローバル) if enable and vec.dot(pos_l,pos_l)>1e-6 then rot_l=mat.rot(gN(4),gN(5),gN(6)) -- リーダー機の回転行列 v_l={gN(7),gN(8),gN(9)} -- リーダー機の速度 (リーダー機ローカル) v_l_g=mat.vec(rot_l,v_l) -- リーダー機の速度 (グローバル) angv_l={gN(10),gN(11),gN(12)} -- リーダー機の角速度 (グローバル) pos_s={gN(13),gN(14),gN(15)} -- 自機の位置 (グローバル) rot_s=mat.rot(gN(16),gN(17),gN(18)) -- 自機の回転行列 rot_s_t=mat.t(rot_s) -- 自機の回転行列の逆 v_s={gN(19),gN(20),gN(21)} -- 自機の速度 (自機ローカル) relative_pos={gN(22),gN(23),gN(24)} -- 相対位置ベクトル (リーダー機ローカル) rot_diff=mat.vec(rot_s_t,mat.rot_vec(mat.mul(rot_l,rot_s_t))) -- 自機とリーダー機の姿勢差分 function to_local_pos(a) return mat.vec(rot_s_t,vec.sub(a,pos_s)) end true_target=vec.add(pos_l,mat.vec(rot_l,relative_pos)) -- 真目標位置 (グローバル) true_target_dist=vec.len(vec.sub(true_target,pos_s)) -- 真目標位置までの距離 target_mul=1+0.25*math.max(true_target_dist-2,0)/vec.len(relative_pos) -- 接近用係数 relative_pos_g=mat.vec(rot_l,vec.mul(relative_pos,target_mul)) -- 係数を掛けた相対位置ベクトル (グローバル) target=vec.add(pos_l,relative_pos_g) -- 係数を掛けた目標位置 (グローバル) from_target=mat.vec(mat.t(rot_l),vec.sub(pos_s,target)) -- 目標位置から見た自機の位置 lead_t=clamp(10*(vec.len(from_target)/vec.len(v_l)),2,30) -- 未来の予測目標位置をとるための先読み時間 t nose_target=vec.add(target,vec.mul(vec.add(v_l_g,vec.mul(vec.cross(angv_l,v_l_g),lead_t/2)),lead_t)) -- 未来の予測目標位置 (グローバル) nose_target_local=to_local_pos(nose_target) -- 未来の予測目標位置 (自機ローカル) control_axis=vec.cross(vec.normalize(v_s),nose_target_local) -- 機首の目標回転軸 roll_control=0.8*rot_diff[3] -- ロールはリーダー機に合わせる pitch_control=control_axis[1] -- ピッチは未来の予測目標位置に合わせる yaw_control=control_axis[2] -- ヨーは未来の予測目標位置に合わせる target_velocity=vec.add(v_l_g,vec.cross(angv_l,relative_pos_g)) -- 編隊成立時の速度 throttle_control=mat.vec(mat.t(rot_s),target_velocity)[3]-v_s[3]-clamp(1*from_target[3],-20,20) -- 補正済み目標速度と現在速度の偏差 sB(1,true) sN(1,roll_control) sN(2,pitch_control) sN(3,yaw_control) sN(4,throttle_control) else sB(1,false) sN(1,0) sN(2,0) sN(3,0) sN(4,0) end end
おわりに
以上のようにして Stormworks の飛行機に自動編隊飛行制御を組み込みました。今回の機体をワークショップに公開しています。操作方法の説明等が用意できていませんが、スイッチ類にはほぼすべてラベルをつけてありますのでご容赦ください。次の手順で編隊飛行を試せます。
- 1機目をスポーン、後席右側の Formation Leader フリップスイッチをオンにする
- 前席に移動し、エンジンを始動して待つ
- 上矢印キーでスロットルを上げ、Sキーで機首を上げて離陸
- 速度を抑え(150~200kt 程度)、水平飛行にする
- 無操作で水平飛行していることを確認したらワークベンチに戻り、2機目をスポーン
- 後席右側の Formation Follower フリップスイッチをオンにする
- 離陸して1機目を追いかける
- 接近すると制御が切り替わり、自動的に1機目に接近して編隊飛行する
解説が拙いこと、細かい部分は本記事で解説しきれていない部分があること、ベクトル・行列計算をフィーリングで適当にやっていることなどツッコミどころは多々あるかと思います。制御自体も、1人で編隊飛行が楽しめそうに思えて離陸は自動化していないため1人で試そうとするといろいろと面倒だったり、アクティブに衝突を回避する機能がなかったり等、課題がまだ多くあります。自分ならもっとうまくやれると思った方はぜひ、来年のアドベントカレンダーにもっと良い自動編隊飛行制御の記事を寄せてください。
おまけ: 行列計算 Lua
実際は上記のメイン Lua の前に最低限のベクトル・行列計算関数を用意しています。その内容も載せておきます。
-- ベクトル・行列計算 vec,mat={},{} function vec.add(a,b) return {a[1]+b[1],a[2]+b[2],a[3]+b[3]} end function vec.sub(a,b) return {a[1]-b[1],a[2]-b[2],a[3]-b[3]} end function vec.mul(a,s) return {a[1]*s,a[2]*s,a[3]*s} end function vec.dot(a,b) return a[1]*b[1]+a[2]*b[2]+a[3]*b[3] end function vec.cross(a,b) return { a[2]*b[3]-a[3]*b[2], a[3]*b[1]-a[1]*b[3], a[1]*b[2]-a[2]*b[1] } end function vec.len(a) return math.sqrt(vec.dot(a,a)) end function vec.normalize(a) l=vec.len(a) if l==0 then return {0,0,0} end return vec.mul(a,1/l) end -- 行列の積 function mat.mul(a,b) local r = {} for i=1,3 do r[i]={} for j=1,3 do r[i][j]=0 for k=1,3 do r[i][j]=r[i][j]+a[i][k]*b[k][j] end end end return r end -- 行列とベクトルの積 function mat.vec(a,b) return { a[1][1]*b[1]+a[1][2]*b[2]+a[1][3]*b[3], a[2][1]*b[1]+a[2][2]*b[2]+a[2][3]*b[3], a[3][1]*b[1]+a[3][2]*b[2]+a[3][3]*b[3] } end -- 行列の転置 function mat.t(a) return { {a[1][1],a[2][1],a[3][1]}, {a[1][2],a[2][2],a[3][2]}, {a[1][3],a[2][3],a[3][3]} } end -- Physics Sensor のオイラー角から回転行列へ function mat.rot(x,y,z) cx,cy,cz=math.cos(x),math.cos(y),math.cos(z) sx,sy,sz=math.sin(x),math.sin(y),math.sin(z) Rx={{1,0,0},{0,cx,-sx},{0,sx,cx}} Ry={{cy,0,sy},{0,1,0},{-sy,0,cy}} Rz={{cz,-sz,0},{sz,cz,0},{0,0,1}} return mat.mul(mat.mul(Rz,Ry),Rx) end -- 回転行列から回転軸ベクトル function mat.rot_vec(r) trace=r[1][1]+r[2][2]+r[3][3] cos_theta=(trace-1)/2 theta=math.acos(clamp(cos_theta,-1,1)) if theta<1e-6 then return {0,0,0} end sin_theta_2=math.sin(theta)*2 return { theta * (r[3][2] - r[2][3])/sin_theta_2, theta * (r[1][3] - r[3][1])/sin_theta_2, theta * (r[2][1] - r[1][2])/sin_theta_2 } end